Régression linéaire en python

ExempleRégression linéaire en python

Voici un premier exemple de régression linéaire en python en utilisant l'algorithme de descente du gradient :

1
import numpy as np
2
3
class Model:
4
    def __init__(self, a, b):
5
        self.a = a
6
        self.b = b
7
    def f(self, x):
8
        return self.a * x + self.b
9
    def __call__(self, x, y):
10
        derreur_df = (2 * ( self.a * x + self.b - y )) 
11
        dJ_da = np.mean(derreur_df * x )
12
        dJ_db = np.mean(derreur_df)
13
        return dJ_da, dJ_db
14
def perte(model,x,y):
15
    return np.mean((model.f(x)-y) ** 2)
16
    
17
x = np.array([1,2,3,4],np.float32)
18
y = np.array([3,5,7,10],np.float32)
19
alpha = 0.005
20
norme_epsilon= 1000
21
seuil_epsilon = 12
22
ma_fonction = Model(7.3, 5.5 )
23
chemin =list()
24
for i in range(1000):
25
    dJ_da, dJ_db = ma_fonction(x, y)
26
    norme_epsilon = np.abs(dJ_da) + np.abs(dJ_db)
27
    ma_fonction.a  = ma_fonction.a - alpha * dJ_da
28
    ma_fonction.b  = ma_fonction.b - alpha * dJ_db
29
print('Perte : ', ma_fonction.b,perte(ma_fonction, x, y))
30
print('(a, b) : (', ma_fonction.a,', ',ma_fonction.b,')')
ExempleComplément du programme précédent
L'exemple précédent ne faisait que la recherche d'une solution en utilisant la descente du gradient. Le programme suivant illustre graphiquement cette méthode :
1
import numpy as np
2
import matplotlib as mpl
3
from mpl_toolkits.mplot3d import Axes3D
4
from matplotlib import pyplot as plt
5
6
class Model:
7
    def __init__(self, a, b):
8
        self.a = a
9
        self.b = b
10
    def f(self, x):
11
        return self.a * x + self.b
12
    def __call__(self, x, y):
13
        derreur_df = (2 * ( self.a * x + self.b - y )) 
14
        dJ_da = np.mean(derreur_df * x )
15
        dJ_db = np.mean(derreur_df)
16
        return dJ_da, dJ_db
17
def perte(model,x,y):
18
    return np.mean((model.f(x)-y) ** 2)
19
    
20
x = np.array([1,2,3,4],np.float32)
21
y = np.array([3,5,7,10],np.float32)
22
alpha = 0.005
23
norme_epsilon= 1000
24
seuil_epsilon = 12
25
ma_fonction = Model(7.3, 5.5 )
26
chemin =list()
27
for i in range(1000):
28
    dJ_da, dJ_db = ma_fonction(x, y)
29
    norme_epsilon = np.abs(dJ_da) + np.abs(dJ_db)
30
    ma_fonction.a  = ma_fonction.a - alpha * dJ_da
31
    ma_fonction.b  = ma_fonction.b - alpha * dJ_db
32
    chemin.append([ma_fonction.a, ma_fonction.b,perte(ma_fonction, x, y)])
33
34
    
35
aa = np.arange(-5 + ma_fonction.a, 5 + ma_fonction.a, 0.05)
36
bb = np.arange(-5 + ma_fonction.b, 5 + ma_fonction.b, 0.05)
37
a_, b_ = np.meshgrid(aa, bb)
38
zz = np.zeros(a_.shape,np.float32)
39
for idx in range(x.shape[0]):
40
    zz = zz + (a_ * x[idx] + b_ - y[idx]) ** 2
41
plt.figure(1)
42
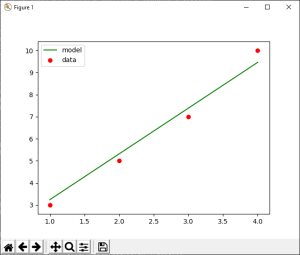
plt.plot(x, ma_fonction.f( x) , c='g')
43
plt.scatter(x, y, c='r')
44
plt.legend(['model', 'data'])
45
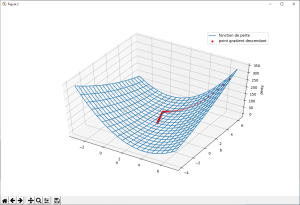
fig = plt.figure(2)
46
ax = fig.gca(projection='3d')
47
surf = ax.plot_wireframe(a_, b_, zz/x.shape[0],
48
                       rstride=10, cstride=10)
49
ax.plot([x[0] for x in chemin], [x[1] for x in chemin], [x[2] for x in chemin], label='gradient descendant')
50
ax.scatter([x[0] for x in chemin], [x[1] for x in chemin], [x[2] for x in chemin],c='r')
51
ax.legend()
52
plt.show()
Ce  graphique montre l'ajustement obtenu.
La fonction de perte en fonction des coefficients a et b de la droite et la trajectoire suivie lors de de la descente du gradient.
ExempleRégression linéaire par moindre carré en utilisant python
Ce programme permet d'obtenir la meilleure équation de droite au sens des moindres carrés.
1
def reglin(x, y):
2
# Calcul de l'équation  de la droite y= a x + b  en utilisant les moindres carrés
3
    m = np.ones((x.shape[0],2),np.float32)
4
    m[:,0]=x.transpose()
5
    p = np.matmul(np.matmul(np.linalg.inv(np.matmul(m.transpose(),m)),m.transpose()),y.reshape(x.shape[0],1))
6
    return p[0,0], p[1,0]
7
8
x = np.array([1,2,3,4],np.float32)
9
y = np.array([3,5,7,10],np.float32)
10
a_mc2, b_mc2 = reglin(x,y)
11
model_ref = Model(a_mc2,b_mc2)
12
print('Perte MC22: ', perte(model_ref(x), y).numpy())
13