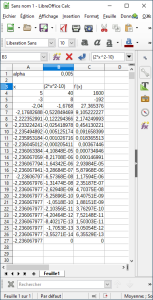
Exemple de descente du gradient
Rappel :
On veut minimiser la fonction f(x), c'est à dire rechercher pour qu'elle valeur de x f(x) est minimum.
Méthode : Algorithme du gradient ou de descente du gradient
On se donne un point initial x0 et un seuil de tolérance ε ⩾ 0. L'algorithme est le suivant :
calcul de \(\nabla f(x_k)\) gradient de la fonction f
si \(||\nabla f(x_k)||<\epsilon \) alors arrêt : xk est une valeur approchée du minimum de f(x)
\(x_{k+1} = x_k - \alpha_k \nabla f(x_k)\)
la valeur \( \alpha_k\) peut être une constante ou bien une valeur variable ajustée au fil des itérations
Exemple : Minimisation de la fonction (2x^2-10)^2
On peut utiliser l'algorithme du gradient dans un tableur pour cette exemple simple.
En python cela nous donne le programme suivant :
1
import numpy as np
2
alpha = 0.005
3
x = 5.0
4
norme_epsilon= 100
5
seuil_epsilon = 0.001
6
while norme_epsilon > seuil_epsilon:
7
f_x = 2 * x ** 2 - 10
8
dfx_dx = 2 * f_x * 4 * x
9
norme_epsilon = np.abs(dfx_dx)
10
x = x - alpha * dfx_dx
11
print(x)
12
ou bien avec une classe :
1
import numpy as np
2
3
class Model():
4
def __call__(self, x):
5
return 2 * (2 * x ** 2 - 10) * 4 * x
6
alpha = 0.005
7
x = 5.0
8
norme_epsilon= 100
9
seuil_epsilon = 0.001
10
ma_fonction = Model()
11
while norme_epsilon > seuil_epsilon:
12
dfx_dx = ma_fonction(x)
13
norme_epsilon = np.abs(dfx_dx)
14
x = x - alpha * dfx_dx
15
print(x)
16
Fondamental : Méthode de la descente du gradient
Minimisation de perte - descente de gradient - gradient stochastique