Approximation d'une fonction en utilisant son développement en série de Fourier
Approximation d'une fonction en utilisant les séries de Fourier
Une fois le développement de la fonction série de Fourier connu, on peut utiliser les termes d'amplitudes supérieur à une valeur donnée pour obtenir une approximation de la fonction. Plus simplement, on peut retenir les termes entiers allant de -n à n pour reconstruire la fonction. Cette reconstitution de la fonction constitue une approximation de la fonction.
Rappel : Série de Fourier
\(f(t)=\sum\limits_{n=-\infty}^{+\infty}c_ne^{i2\pi \frac{n}{T}t}\) avec \(c_n = \frac{1}{T}\int\limits_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-i2\pi \frac{n}{T}t}dt\)
Méthode : Approximation de la fonction en utilisant les séries de Fourier
La sommation ne se fait plus de \(-\infty\) à \(+\infty\) mais de -N à +N.
\(f(t) \approx \sum\limits_{n=-N}^{+N}c_ne^{i2\pi \frac{n}{T}t}\)
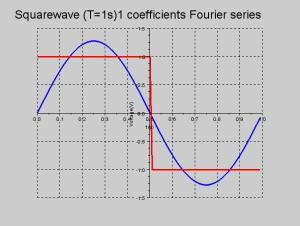
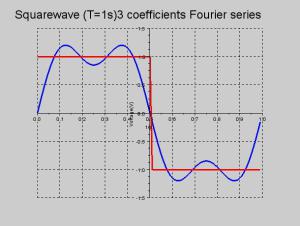
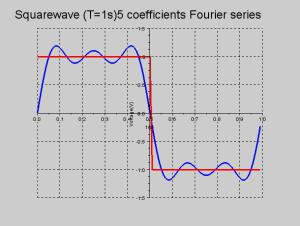
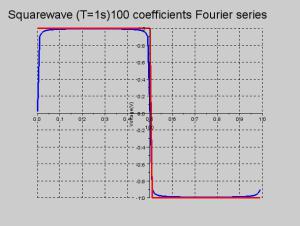
Exemple : Approximation du signal carré
Approximation en utilisant 3 coefficients
\(\sqcap_T(t) \approx \sum\limits_{n=-1}^{+1}c_ne^{i2\pi \frac{n}{T}t}=4\frac{\sin \frac{2\pi t}{T}}{\pi }\)
Approximation en utilisant 7 coefficients
\(\sqcap_T(t) \approx \sum\limits_{n=-3}^{+3}c_ne^{i2\pi \frac{n}{T}t}=\frac{4\sin\frac{2\pi t}{T}}{\pi }+\frac{4\sin \frac{6\pi t}{T}}{3\pi}\)
Approximation en utilisant 11 coefficients
\(\sqcap_T(t) \approx \sum\limits_{n=-5}^{+5}c_ne^{i2\pi \frac{n}{T}t}=\frac{4\sin\frac{2\pi t}{T}}{\pi }+\frac{4\sin \frac{6\pi t}{T}}{3\pi}+\frac{4\sin \frac{10\pi t}{T}}{5\pi}\)
Approximation en utilisant 201 coefficients
\(\sqcap_T(t) \approx \sum\limits_{n=-100}^{+100}c_ne^{i2\pi \frac{n}{T}t}\)
Exemple : Construction d'une fonction à partir des coefficient s de la série de Fourier
Dans l'exemple suivant, vous allez choisir les coefficients \(c_{-2}, c_{-1}, c_0, c_1, c_2\) de la série de Fourier pour calculer une fonction f(t) . La fonction obtenue sera alors calculée à partir de la formule :
\(f(t)=\sum_{n=-\infty}^{+\infty}c_ne^{i\frac{2\pi n}{T}}\)
A partir de la fenêtre précédente vous pouvez vérifier quelques propriétés des coefficients \(c_n\) de la série de Fourier :
f(t) est une fonction réelle alors \(c_n=c^*_{-n}\) où c* désigne le conjugué de c (c=x+iy alors c*=x-iy)
f(t) est paire alors \(c_n=c_{-n}\)
f(t) est impaire alors \(c_n=-c_{-n}\)
Remarque : Approximation et compression de signaux
Cette technique est utilisée pour compresser un signal.