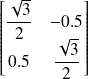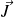Coordonnées homogènes dans le plan
Définition : Matrice
Une matrice est un tableau de nombres, utilisée plus particulièrement en algèbre linéaire.
Définition : Addition de deux matrices
Addition :
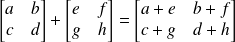
On peut additionner deux matrices si leurs tailles, nombre de lignes et de colonnes, sont identiques.
La règle générale est
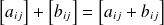
où
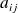 désigne l'élement de la matrice en ligne i et colonne j.
désigne l'élement de la matrice en ligne i et colonne j.
Définition : Produit de deux matrices
Produit matriciel :
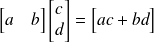
La règle générale est
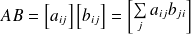
Si A a n lignes et m colonnes et B a p lignes et q colonnes alors le produit de A par B a N lignes et q colonnes et le nombre de colonnes de A doit être égal au nombre de lignes de B m=p.
Exemple : Exemple de produits matriciel
Quelques exemples :
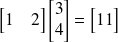
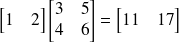
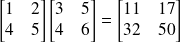
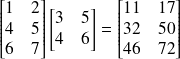
Définition : Transposée d'une matrice
La transposée d'une matrice est obtenue en échangeant les lignes et les colonnes.
Si
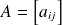 alors la transposée de A notée
alors la transposée de A notée
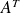 est égale à
est égale à
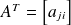
Rappel : produit scalaire de deux vecteurs
Soient deux vecteurs de composantes
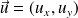 et
et
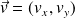 le produit scalaire de
le produit scalaire de
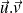 est égal à
est égal à
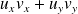 .
.
Il peut se mettre sous la forme matricielle suivante :
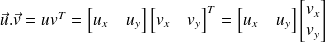
Définition : Droite
Une droite dans le plan est définie par l'équation :
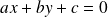
Remarque : Droite et points sous forme matricielle
Un point A
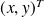 appartient à la droite D d'équation ax+by+c si
appartient à la droite D d'équation ax+by+c si
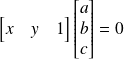
Un point dans le plan est représenté un vecteur à 3 composantes.
Si le point de coordonnées
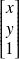 appartient à la droite alors le point de coordonnées
appartient à la droite alors le point de coordonnées
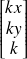 appartient aussi à la droite.
appartient aussi à la droite.
Un point de coordonnées
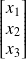 représente donc un point du plan
représente donc un point du plan
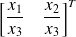
Définition : Produit vectoriel
Le produit vectoriel de deux vecteurs
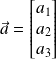
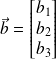 est égal à :
est égal à :
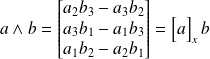 avec
avec
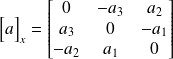
Définition : Intersection de deux droites du plan
Deux droites
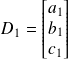 et
et
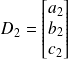 se coupent en un Point M dont les coordonnées homogènes sont
se coupent en un Point M dont les coordonnées homogènes sont
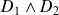
Exemple : Intersection de droites
Soient deux droites d'équation x+y+3=0 et 2x+y+1=0.
L'intersection de ces droites est donnée par le produit vectoriel de [1 1 3] et [2 1 1].
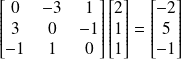 soit en coordonnées homogènes le point
soit en coordonnées homogènes le point

Exemple : Intersection de droites parallèles
Soient deux droites d'équation x+y+3=0 et x+y+5=0.
L'intersection de ces droites est donnée par le produit vectoriel de [1 1 3] et [1 1 5].
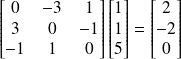 soit en coordonnées homogènes le point
soit en coordonnées homogènes le point
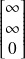 Le point est à l'infini !
Le point est à l'infini !
Remarque : Deux droites parallèles se coupent à l'infini ?
Cette propriété peut sembler mathématique mais a deux nombreuses applications pratiques en dessin comme en traitement d'images.
Les droites parallèles dans le monde réel se coupent avant l'infini dans une perspective. Les droites parallèles doivent converger vers le même point (point de fuite) |
Les droites [1 2 3] et [1 2 5]. se coupent à l'infini en [2 -1 0].
Définition : Matrice de passage et changement de repère
Soit une base B1=(e1,...,en) et d'une base B2=(f1,...,fn). On appelle matrice de passage de B1 à B2 la matrice carrée de taille n dont la j-ième colonne est formée des coordonnées de fj dans la base B1. Autrement dit, la matrice de passage de B1 à B2 est la matrice des nouveaux vecteurs de base exprimés en fonction des anciens.
Soit e un vecteur de E, X1 ses coordonnées dans B1, X2 ses coordonnées dans B2, et soit P1,2 la matrice de passage de B1 à B2. Alors on a :
X1=P1,2X2
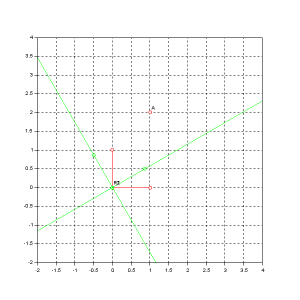
Exemple : Rotation de 90°
Le repère B1 est
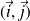 et le repère B2 est
et le repère B2 est
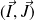 avec
avec
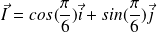 et
et
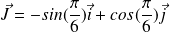
La matrice de passage est donc :
Dans la première colonne on retrouve les coordonnées de
|
Les coordonnées dans B2 de
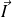 =[1 0]T sont dans B1 données par la relation matricielle :
=[1 0]T sont dans B1 données par la relation matricielle :
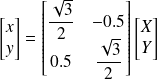
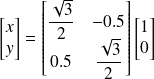
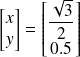
Les coordonnées dans B1 de
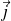 =[0 1]T sont dans B2 données par la relation matricielle :
=[0 1]T sont dans B2 données par la relation matricielle :
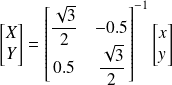
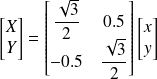
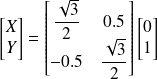
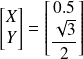
Définition : Changement de repère en coordonnées homogènes
En coordonnées homogènes l'origine du repère peut être déplacé. On ajoute une colonne, la translation associée au déplacement, à la matrice de passage. Si la matrice de passage pour passer du repère B1 à B2 est
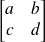 et la vecteur translation [tx ty^]T alors la matrice de passage sera :
et la vecteur translation [tx ty^]T alors la matrice de passage sera :
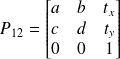
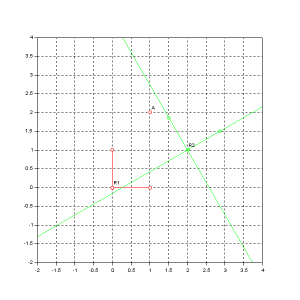
Exemple : Changement de repère dans le plan
On reprend l'exemple précédent :
Le repère B1 est
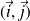 et le repère B2 est
et le repère B2 est
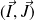 avec
avec
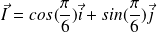 et
et
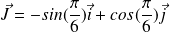
on ajoute une translation de vecteur
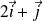 . la matrice de passage est donc :
. la matrice de passage est donc :
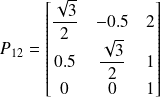
Soit un point, de coordonnées [x1 y1 1]T dans B1, de coordonnées de coordonnées [x2 y2 1]T dans B2, et soit P1,2 la matrice de passage de B1 à B2. Alors on a : [x1 y1 1]T=P12[x2 y2 1]T Par exemple l'origine du repère B2 a pour coordonnées P12[0 0 1]T dans B1, soit [2 1 1]T. De même l'origine du repère B1 a pour coordonnées P12(-1)[0 0 1]T dans B1, soit environ [-2.232 0.134 1]T. |